While building and teaching my course this summer on Fourier analysis, I pulled apart something called Gibb's phenomenon. This is a remarkable quirk of Fourier series: they overshoot the function at jump discontinuities, and what's interesting is that the overshoot is always close to 9% of the jump discontinuity. I heard about this when I was in college, but never knew why this works. Here, we'll look at a simple example, where we will be able to prove that the overshoot is 9%, regardless of how many terms in the Fourier series are added. The proof will be some work, but not difficult to understand with the needed background in calculus.
The example we will detail is the "square wave" function \(f\), defined on the interval \((-\pi,\pi]\) by \[ f(x) = \left\{\begin{array}{rlr} 1 &\text{ if } & 0\le x \le\pi \\ -1 &\text{ if } & -\pi\lt x\lt 0\end{array}\right.\] and then extended to be \(2\pi\)-periodic on the real number line.
The Fourier series happens to be: \[ f(x) = \frac{4\sin x}{\pi} + \frac{4\sin 3x}{3\pi} + \frac{4\sin 5x}{5\pi} + \frac{4\sin 7x}{7\pi} + \cdots \]
If we plot partial sums of the Fourier series, Gibb's phenomenon becomes apparent:
Here's a plot with 10 terms:
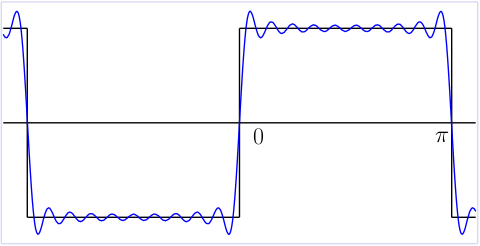
Here's a plot with 50 terms:
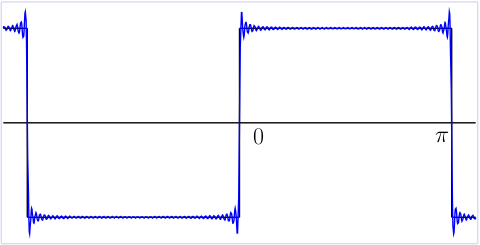
To find the height of the overshoot, we look for the first maximum point of the partial sum of the first \(n\) terms of the Fourier series. We will do this simply by finding the derivative and setting that to zero, just as in ordinary calculus.
The sum of the first \(n\) terms is: \[ g(x) = \frac{4}{\pi}\left( \sin x + \frac{\sin 3x}{3} + + \frac{\sin 5x}{5} + \cdots + \frac{\sin ((2n-1)x)}{2n-1} \right) \]
The derivative of this is \[ g'(x) = \frac{4}{\pi}\big( \cos x + \cos 3x + \cos 5x + \cdots + \cos((2n-1)x) \big)\]
Now the hard part: setting this to zero and solving for \(x\).
The trick is to first find a formula for this sum.
Let's look at the sum of just the cosine terms: \[ S = \cos x + \cos 3x + \cos 5x + \cdots + \cos((2n-1)x)\]
Multiply this by \(\sin x\): \[ S\sin x = \cos x\sin x + \cos 3x\sin x + \cos 5x\sin x + \cdots + \cos((2n-1)x)\sin x\]
Now use the product-to-sum identity \[ \cos \alpha\sin\beta = \tfrac12\sin(\alpha+\beta)-\tfrac12\sin(\alpha-\beta)\] to rewrite each term of the sum as differences of sines: \[ \begin{align*} S\sin x &= \left(\tfrac12\sin 2x - \tfrac12\sin 0\right) + \left(\tfrac12\sin 4x - \tfrac12\sin 2x\right) + \left(\tfrac12\sin 6x - \tfrac12\sin 4x\right) + \cdots \\ & \quad\quad + \left(\tfrac12\sin((2n-2)x) - \tfrac12\sin((2n-4)x)\right) \\ & \quad\quad + \left(\tfrac12\sin(2nx) - \tfrac12\sin((2n-2)x)\right) \end{align*}\]
This now telescopes—everything cancels except one term: \[ S\sin x = \tfrac12\sin(2nx)\]
This finally gives \[ S = \frac{\sin(2nx)}{2\sin x}.\]
Now we can set the sum equal to zero and solve for \(x\): \[ S = \frac{\sin(2nx)}{2\sin x} = 0\]
The first positive zero is \(x\) such that \(2nx=\pi\). This is \[ x = \frac{\pi}{2n}.\]
We need to find the \(y\)-coordinate of the first maximum. So we put this \(x\) into the partial sum itself.
The partial sum is \[ \begin{align*} g(x) &= \frac{4}{\pi}\left( \sin x + \frac{\sin 3x}{3} + \frac{\sin 5x}{5} + \cdots + \frac{\sin ((2n-1)x)}{2n-1} \right) \\ &= \frac{4}{\pi}\sum_{k=1}^n \frac{\sin((2k-1)x)}{2k-1}. \end{align*} \]
This gives \[ g\left(\frac{\pi}{2n}\right) = \frac{4}{\pi}\sum_{k=1}^n \frac1{2k-1}\sin\left(\frac{(2k-1)\pi}{2n}\right) \]
Now we rewrite the sum (we multiply and divide by \(n\), and do a bit of algebra):
\[ g\left(\frac{\pi}{2n}\right) = \sum_{k=1}^n \frac{2}{\pi}\left(\frac{(2k-1)\pi}{2n}\right)^{-1}\sin\left(\frac{(2k-1)\pi}{2n}\right)\,\frac\pi{n} \]We will verify this is a Riemann sum for the following integral: \[ \frac2\pi\int_0^\pi x^{-1}\sin x\, dx = \frac2\pi\int_0^\pi \frac{\sin x}{x}\, dx \]
The template for Riemann sums is \[ \int_a^b f(x)\, dx \approx \sum_{k=1}^n f(x_k^*)\, \Delta x,\] where the interval \([a,b]\) has been cut into \(n\) equal subintervals \([x_{k-1},x_k]\), and \(x_k^*\) is a sample point from the \(k\)th subinterval.
Here, we have \[ \Delta x = \frac{b-a}n = \frac{\pi-0}n = \frac{\pi}{n}\] and (for \(0\le k\le n\)) \[ x_k = a + k\,\Delta x = 0 + k(\pi/n)=\frac{\pi k}n.\]
Now let \(x_k^*\) be the midpoint of the \(k\)th subinterval. This turns out to be \[ x_k^* = \frac{x_{k-1}+x_k}2 = \frac12\left(\frac{\pi(k-1)}n + \frac{\pi k}n\right) = \left(k-\frac12\right)\frac\pi{n} = \frac{(2k-1)\pi}{2n}.\]
So we get \[ \sum_{k=1}^n f(x_k^*)\, \Delta x = \sum_{k=1}^n \frac{2}{\pi}\left(\frac{(2k-1)\pi}{2n}\right)^{-1}\sin\left(\frac{(2k-1)\pi}{2n}\right)\,\frac\pi{n} \]
So the sum is exactly the Riemann sum for the integral.
The upshot of this is that the \(y\)-coordinate of the first maximum is approximated by the integral: \[ g\left(\frac{\pi}{2n}\right) \approx \frac2\pi\int_0^\pi \frac{\sin x}{x}\, dx \approx 1.17898.\]
The jump discontinuity is from \(-1\) up to \(1\) at \(x=0\), a jump of \(2\).
The overshoot above \(y=1\) is \(1.17898-1 = 0.17898\).
So the percent overshoot is this number divided by \(2\): \[ \frac12\left(\frac2\pi\int_0^\pi \frac{\sin x}{x}\, dx - 1\right) = \frac{1.17898-1}2 = 0.08949\] or 8.949% (rounded).
This exact same value for the percent overshoot holds for any function with a jump discontinuity. But at least for this function, we can see why this works, and where this odd number comes from.